Chào các em, các bậc phụ huynh và những ai đang tìm hiểu về môn Toán lớp 4 đầy thú vị! Hôm nay, chúng ta sẽ cùng nhau khám phá một kiến thức cực kỳ quan trọng và hữu ích: cách tính Diện Tích Hình Thoi Lớp 4. Nghe có vẻ đơn giản, nhưng để thực sự hiểu sâu và áp dụng thành thạo, chúng ta cần đi vào từng ngóc ngách nhỏ nhất. Hãy cùng BSS Việt Nam lật mở bí ẩn đằng sau công thức tính diện tích hình thoi này nhé.
Chắc hẳn trong cuộc sống, em đã từng bắt gặp hình ảnh chiếc diều bay lượn trên bầu trời, hay những họa tiết trang trí trên áo, trên gạch lát nền nhà. Rất có thể, đó chính là hình thoi đấy! Hình thoi xuất hiện quanh ta nhiều hơn chúng ta tưởng, và việc biết cách tính diện tích của nó không chỉ giúp em giải quyết bài tập trên lớp mà còn mở ra cách nhìn mới về thế giới hình học phẳng.
Học cách tính diện tích hình thoi lớp 4 không chỉ là ghi nhớ một công thức khô khan. Đó là cả một hành trình khám phá, từ việc nhận diện hình thoi, hiểu rõ đặc điểm của nó, cho đến việc suy luận ra công thức một cách logic. Giống như khi xây dựng một ngôi nhà, mỗi viên gạch kiến thức đều quan trọng. Nắm chắc kiến thức cơ bản như diện tích hình thoi lớp 4 sẽ là nền tảng vững chắc giúp em chinh phục những bài toán khó hơn sau này, thậm chí là áp dụng vào các tình huống thực tế, từ những điều nhỏ nhặt như cắt giấy thủ công hình thoi đến những ứng dụng phức tạp hơn trong thiết kế hay kỹ thuật.
Để hiểu sâu về một vấn đề, đôi khi chúng ta cần nhìn nó từ nhiều góc độ khác nhau. Điều này làm tôi liên tưởng đến việc phân tích một phát biểu nào sau đây là không đúng? trong logic hoặc kinh doanh. Cần phải xem xét kỹ lưỡng từng khía cạnh, từng giả định để tìm ra sự thật. Với hình thoi cũng vậy, chúng ta không chỉ học công thức, mà còn tìm hiểu “vì sao” lại có công thức đó, “làm thế nào” để áp dụng nó một cách chính xác nhất.
Hình Thoi Là Gì? Đặc Điểm Quan Trọng Của Hình Thoi
Trước khi tính diện tích, chúng ta cần biết rõ “nhân vật chính” của chúng ta là ai, đúng không nào? Hình thoi là một dạng hình tứ giác đặc biệt. Tứ giác tức là hình có bốn cạnh và bốn góc. Vậy, điều gì làm nên sự khác biệt của hình thoi so với các loại tứ giác khác như hình vuông, hình chữ nhật hay hình bình hành?
Những đặc điểm nhận dạng hình thoi vô cùng rõ ràng và thú vị:
- Bốn cạnh bằng nhau: Đây là đặc điểm nổi bật nhất! Một khi tứ giác có bốn cạnh dài bằng nhau, nó chắc chắn là hình thoi. Hãy tưởng tượng một hình vuông bị “nghiêng” đi một chút, nó sẽ trở thành hình thoi (trừ trường hợp nó vẫn là hình vuông).
- Các cặp cạnh đối song song: Giống như hình bình hành, các cạnh đối diện của hình thoi luôn song song với nhau. Cạnh này song song với cạnh đối diện của nó.
- Các góc đối bằng nhau: Góc ở đỉnh này sẽ bằng góc ở đỉnh đối diện. Tuy nhiên, các góc kề nhau lại bù nhau (tổng bằng 180 độ), trừ khi nó là hình vuông (khi đó tất cả các góc đều vuông).
- Hai đường chéo vuông góc với nhau: Đây là một đặc điểm rất quan trọng và độc đáo của hình thoi (và hình vuông). Hai đường chéo nối hai cặp đỉnh đối diện sẽ cắt nhau tại một điểm và tạo thành 4 góc vuông tại điểm đó.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Điểm giao nhau của hai đường chéo chia mỗi đường chéo thành hai phần bằng nhau.
- Hai đường chéo là đường phân giác của các góc: Mỗi đường chéo chia đôi góc mà nó đi qua.
Hiểu rõ những đặc điểm này không chỉ giúp em nhận biết hình thoi mà còn là chìa khóa để suy luận ra công thức tính diện tích, như chúng ta sẽ thấy ngay sau đây.
Công Thức Tính Diện Tích Hình Thoi Lớp 4: Chìa Khóa Nằm Ở Đâu?
Giờ thì đến phần mà chúng ta mong chờ nhất! Làm thế nào để tính diện tích hình thoi lớp 4? Công thức cực kỳ đơn giản và dễ nhớ. Nó dựa vào độ dài của hai đường chéo của hình thoi.
Công thức tính diện tích hình thoi là:
Diện tích = (Độ dài đường chéo 1 x Độ dài đường chéo 2) / 2
Hoặc viết bằng ký hiệu toán học:
S = (d₁ x d₂) / 2
Trong đó:
Slà diện tích hình thoi.d₁là độ dài của một đường chéo.d₂là độ dài của đường chéo còn lại.
Rất đơn giản phải không? Chỉ cần biết độ dài của hai đường chéo, thực hiện một phép nhân và một phép chia là em đã có ngay diện tích của hình thoi rồi.
Diện tích hình thoi lớp 4 được tính như thế nào?
Diện tích hình thoi lớp 4 được tính bằng cách lấy tích độ dài hai đường chéo rồi chia cho 2. Công thức này áp dụng cho mọi hình thoi, bất kể kích thước hay hình dạng (miễn là nó đúng là hình thoi).
Đường chéo hình thoi là gì?
Đường chéo hình thoi là đoạn thẳng nối hai đỉnh đối diện của hình thoi. Mỗi hình thoi có chính xác hai đường chéo. Chúng cắt nhau tại trung điểm và vuông góc với nhau.
Vì sao công thức tính diện tích hình thoi lại là tích hai đường chéo chia đôi?
Đây là câu hỏi cực kỳ hay và cho thấy em đang suy nghĩ một cách logic! Việc hiểu nguồn gốc công thức sẽ giúp em nhớ lâu hơn và áp dụng linh hoạt hơn. Có nhiều cách để giải thích điều này, cách phổ biến và dễ hiểu nhất cho học sinh lớp 4 là dựa vào hình chữ nhật.
Hãy cùng tưởng tượng nhé:
- Vẽ một hình thoi bất kỳ.
- Vẽ hai đường chéo của hình thoi đó. Gọi độ dài hai đường chéo là d₁ và d₂.
- Từ các đỉnh của hình thoi, vẽ các đường thẳng song song với hai đường chéo, sao cho chúng cắt nhau tạo thành một hình chữ nhật bao quanh hình thoi ban đầu.
- Quan sát hình em vừa vẽ. Em sẽ thấy hình thoi nằm gọn bên trong hình chữ nhật đó.
- Chiều dài của hình chữ nhật này chính là độ dài của đường chéo dài hơn (d₂), và chiều rộng của hình chữ nhật chính là độ dài của đường chéo ngắn hơn (d₁). (Hoặc ngược lại, tùy cách em đặt tên đường chéo).
- Diện tích của hình chữ nhật bao quanh này là: Chiều dài x Chiều rộng = d₁ x d₂.
- Bây giờ, hãy nhìn kỹ lại mối quan hệ giữa hình thoi và hình chữ nhật bao quanh. Hai đường chéo của hình thoi chia hình thoi thành 4 tam giác vuông nhỏ. Đồng thời, hình chữ nhật bao quanh cũng được chia thành 4 hình chữ nhật nhỏ (bởi hai đường chéo kéo dài). Mỗi tam giác vuông của hình thoi chính là MỘT NỬA của một hình chữ nhật nhỏ tương ứng trong hình chữ nhật lớn.
- Tổng diện tích 4 tam giác vuông (chính là diện tích hình thoi) sẽ bằng tổng diện tích của MỘT NỬA của 4 hình chữ nhật nhỏ. Mà tổng diện tích 4 hình chữ nhật nhỏ chính là diện tích của hình chữ nhật lớn (d₁ x d₂).
- Do đó, diện tích hình thoi bằng một nửa diện tích của hình chữ nhật bao quanh.
- Vậy, Diện tích hình thoi = (d₁ x d₂) / 2.
Thật kỳ diệu phải không nào? Từ một hình dạng tưởng chừng phức tạp như hình thoi, chúng ta lại có thể dựa vào những hình cơ bản hơn như tam giác và hình chữ nhật để tìm ra công thức diện tích. Hiểu được “câu chuyện” đằng sau công thức này giúp em không chỉ học vẹt mà còn phát triển tư duy hình học.
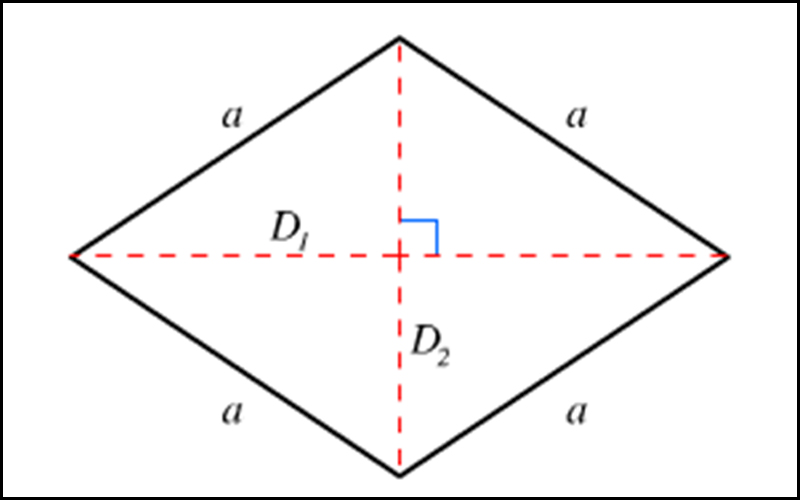Hình minh họa một hình thoi cùng hai đường chéo giúp hiểu công thức diện tích hình thoi lớp 4
Hướng Dẫn Từng Bước Cách Tính Diện Tích Hình Thoi
Đã nắm vững công thức và hiểu nguồn gốc rồi, bây giờ chúng ta sẽ đi vào phần thực hành. Để tính diện tích hình thoi, em chỉ cần làm theo các bước sau:
Bước 1: Xác định độ dài của hai đường chéo.
- Trong bài toán, đề bài sẽ cho em biết độ dài của hai đường chéo. Chúng có thể có đơn vị khác nhau (ví dụ: cm và dm), em cần đổi chúng về cùng một đơn vị đo độ dài trước khi tính toán.
- Nếu đề bài cho hình vẽ, em cần đo độ dài của hai đường chéo đó (tuy nhiên, trong bài tập lớp 4 thường sẽ cho sẵn số liệu).
- Gọi độ dài hai đường chéo lần lượt là d₁ và d₂.
Bước 2: Áp dụng công thức.
- Nhân độ dài của hai đường chéo với nhau: d₁ x d₂.
- Chia kết quả vừa tìm được cho 2: (d₁ x d₂) / 2.
Bước 3: Ghi đơn vị diện tích phù hợp.
- Nếu độ dài đường chéo đo bằng centimet (cm), diện tích sẽ có đơn vị là centimet vuông (cm²).
- Nếu độ dài đường chéo đo bằng mét (m), diện tích sẽ có đơn vị là mét vuông (m²).
- Nếu độ dài đường chéo đo bằng decimet (dm), diện tích sẽ có đơn vị là decimet vuông (dm²).
- Luôn nhớ ghi đơn vị diện tích sau kết quả cuối cùng nhé!
Ví dụ: Một hình thoi có độ dài hai đường chéo lần lượt là 6 cm và 8 cm.
- Bước 1: d₁ = 6 cm, d₂ = 8 cm. (Cùng đơn vị rồi!)
- Bước 2: (6 x 8) / 2 = 48 / 2 = 24.
- Bước 3: Đơn vị là cm, nên diện tích là cm².
- Vậy, diện tích hình thoi là 24 cm².
Thật dễ dàng phải không nào? Chỉ cần làm theo 3 bước này, em có thể tự tin giải mọi bài toán tính diện tích hình thoi lớp 4!
Ví Dụ Thực Tế Về Tính Diện Tích Hình Thoi
Lý thuyết là một chuyện, thực hành lại là chuyện khác. Chúng ta hãy cùng nhau làm vài bài tập ví dụ để “thấm” hơn cách tính diện tích hình thoi lớp 4 nhé!
Ví dụ 1:
Tính diện tích hình thoi có độ dài hai đường chéo là 10 dm và 15 dm.
- Phân tích: Đề bài cho sẵn độ dài hai đường chéo, đơn vị đều là dm. Ta chỉ cần áp dụng công thức.
- Lời giải:
- Diện tích hình thoi là:
- (10 x 15) / 2 = 150 / 2 = 75 (dm²)
- Đáp số: 75 dm²
Ví dụ 2:
Một tấm bìa hình thoi có độ dài đường chéo thứ nhất là 20 cm, độ dài đường chéo thứ hai gấp rưỡi đường chéo thứ nhất. Tính diện tích tấm bìa đó.
- Phân tích: Đề bài cho độ dài đường chéo thứ nhất và mối quan hệ giữa hai đường chéo. Ta cần tính độ dài đường chéo thứ hai trước khi áp dụng công thức.
- Lời giải:
- Độ dài đường chéo thứ hai là:
- 20 x 1.5 = 30 (cm)
- Diện tích tấm bìa hình thoi là:
- (20 x 30) / 2 = 600 / 2 = 300 (cm²)
- Đáp số: 300 cm²
Ví dụ 3:
Tính diện tích hình thoi biết độ dài một đường chéo là 4m và đường chéo còn lại là 30 dm.
- Phân tích: Đề bài cho độ dài hai đường chéo nhưng khác đơn vị (m và dm). Ta cần đổi về cùng một đơn vị. Nên đổi về dm hoặc m đều được, nhưng đổi về dm thường cho số nguyên dễ tính hơn.
- Lời giải:
- Đổi 4m ra dm: 4m = 40 dm.
- Độ dài hai đường chéo là 40 dm và 30 dm.
- Diện tích hình thoi là:
- (40 x 30) / 2 = 1200 / 2 = 600 (dm²)
- Hoặc, đổi 30dm ra m: 30 dm = 3 m.
- Độ dài hai đường chéo là 4m và 3m.
- Diện tích hình thoi là:
- (4 x 3) / 2 = 12 / 2 = 6 (m²)
- Lưu ý: 600 dm² = 6 m², kết quả hoàn toàn khớp nhau!
- Đáp số: 600 dm² (hoặc 6 m²)
Qua ba ví dụ này, em thấy việc áp dụng công thức tính diện tích hình thoi lớp 4 không hề khó chút nào, đúng không? Quan trọng là đọc kỹ đề bài, xác định đúng độ dài hai đường chéo và chú ý đến đơn vị đo.
Ứng Dụng Của Hình Thoi Trong Cuộc Sống Xung Quanh Chúng Ta
Đôi khi, học toán không chỉ để làm bài kiểm tra mà còn để thấy được sự hiện diện của toán học trong đời sống. Hình thoi cũng vậy, nó “ẩn mình” ở rất nhiều nơi đấy!
- Diều: Chiếc diều truyền thống của Việt Nam thường có hình dáng của một hình thoi.
- Họa tiết trang trí: Rất nhiều hoa văn trên gạch lát nền, trên vải vóc, thảm, hoặc đồ trang sức có sử dụng hình thoi.
- Biển báo giao thông: Một số biển báo có hình thoi (mặc dù ít phổ biến ở Việt Nam).
- Kiến trúc: Đôi khi cửa sổ, khung cửa hoặc các chi tiết trang trí trên tường có thể sử dụng hình thoi.
- Kỹ thuật: Trong một số cấu trúc kỹ thuật, hình thoi được sử dụng vì tính đối xứng và độ vững chắc (ở một số góc độ).
- Thiên nhiên: Một số tinh thể hoặc cấu trúc phân tử có thể có dạng hình thoi.
Việc nhận ra hình thoi trong cuộc sống giúp bài học về diện tích hình thoi lớp 4 trở nên sinh động và gần gũi hơn. Toán học không chỉ trên sách vở, nó ở quanh ta mỗi ngày!
Những Lỗi Thường Gặp Khi Tính Diện Tích Hình Thoi Lớp 4 và Cách Khắc Phục
Trong quá trình học và làm bài tập, đôi khi chúng ta vẫn mắc phải những lỗi nhỏ. Biết trước những lỗi này sẽ giúp em cẩn thận hơn. Đối với việc tính diện tích hình thoi lớp 4, có vài điểm cần lưu ý:
- Nhầm lẫn đơn vị đo: Đây là lỗi phổ biến nhất, như trong Ví dụ 3 ở trên. Khi độ dài hai đường chéo không cùng đơn vị, em bắt buộc phải đổi về cùng một đơn vị trước khi tính toán. Hãy kiểm tra kỹ đơn vị của d₁ và d₂ trước khi thực hiện phép nhân.
- Sử dụng nhầm công thức: Đôi khi, các em có thể nhầm lẫn công thức tính diện tích hình thoi với công thức tính diện tích hình chữ nhật (dài x rộng), hình vuông (cạnh x cạnh) hoặc hình bình hành (đáy x chiều cao). Hãy nhớ rõ công thức đặc trưng của hình thoi là (d₁ x d₂) / 2.
- Quên chia cho 2: Công thức có phép chia cho 2 ở cuối. Đôi khi làm bài nhanh, em có thể quên mất bước này và chỉ nhân hai đường chéo với nhau. Kết quả sẽ sai gấp đôi!
- Ghi sai đơn vị diện tích: Diện tích luôn phải có đơn vị vuông (cm², m², dm²,…). Đừng quên ký hiệu số 2 nhỏ ở trên đơn vị nhé.
- Nhầm lẫn đường chéo với cạnh: Đường chéo là đoạn nối hai đỉnh đối diện, còn cạnh là đoạn nối hai đỉnh kề nhau. Công thức diện tích hình thoi sử dụng độ dài đường chéo, không phải độ dài cạnh.
Để khắc phục những lỗi này, hãy luôn đọc đề bài cẩn thận, gạch chân các thông tin quan trọng (độ dài đường chéo, đơn vị), và viết rõ công thức ra nháp trước khi bắt đầu tính toán. Kiểm tra lại các bước sau khi tính xong là cách tốt nhất để đảm bảo kết quả chính xác.
Giống như trong kinh doanh, một nền tảng số là gì vững chắc giúp doanh nghiệp phát triển. Trong học toán, việc nắm chắc kiến thức cơ bản và tránh các lỗi thường gặp chính là xây dựng nền tảng vững chắc cho mình.
Làm Thế Nào Để Nhớ Lâu Công Thức Tính Diện Tích Hình Thoi?
Việc ghi nhớ công thức đôi khi là thử thách, nhưng có nhiều cách để làm cho nó dễ dàng hơn.
- Hiểu nguồn gốc: Như chúng ta đã phân tích ở phần giải thích vì sao công thức là (d₁ x d₂) / 2 dựa trên hình chữ nhật bao quanh. Khi em hiểu được “câu chuyện” này, công thức sẽ trở nên có ý nghĩa hơn và khó quên hơn.
- Liên hệ với các hình khác: So sánh công thức diện tích hình thoi với các công thức diện tích khác mà em đã học (hình chữ nhật, hình vuông, hình bình hành). Tìm ra điểm giống và khác nhau sẽ giúp em phân biệt.
- Thực hành thường xuyên: Làm thật nhiều bài tập! Đây là cách tốt nhất để “khắc sâu” công thức vào trí nhớ. Bắt đầu với các bài đơn giản, sau đó thử sức với các bài khó hơn có lồng ghép thêm các yếu tố khác.
- Tạo flashcard: Viết công thức lên một mặt của tấm thẻ, mặt còn lại vẽ hình thoi và ghi chú các đường chéo. Ôn tập hàng ngày.
- Dạy lại cho người khác: Thử giải thích công thức và cách tính cho bạn bè, em hoặc bố mẹ. Khi em có thể giải thích cho người khác, điều đó chứng tỏ em đã hiểu rất rõ.
- Áp dụng vào thực tế: Thử tìm các vật dụng hình thoi quanh nhà và tưởng tượng cách em tính diện tích của chúng (nếu biết độ dài đường chéo).
Bằng cách kết hợp nhiều phương pháp, em sẽ thấy việc ghi nhớ và vận dụng công thức tính diện tích hình thoi lớp 4 trở nên nhẹ nhàng và hiệu quả hơn rất nhiều.
Minh họa cách giải thích công thức tính diện tích hình thoi lớp 4 bằng hình chữ nhật
Kết Nối Kiến Thức Diện Tích Hình Thoi Với Các Hình Khác
Học toán là một chuỗi liên tục, kiến thức này là nền tảng cho kiến thức khác. Việc học diện tích hình thoi lớp 4 có liên quan mật thiết đến các kiến thức về hình học mà em đã hoặc sẽ học:
- Hình Tứ giác: Hình thoi là một trường hợp đặc biệt của hình tứ giác.
- Hình Bình hành: Hình thoi cũng là một trường hợp đặc biệt của hình bình hành (hình bình hành có bốn cạnh bằng nhau). Công thức diện tích hình bình hành là đáy x chiều cao. Em có thể thử suy nghĩ làm thế nào để liên hệ công thức này với công thức diện tích hình thoi? (Đây là một bài tập nâng cao hơn nhé).
- Hình Chữ nhật: Như đã nói, công thức diện tích hình thoi có thể suy luận từ diện tích hình chữ nhật bao quanh.
- Hình Vuông: Hình vuông là trường hợp đặc biệt của hình thoi (hình thoi có bốn góc vuông). Nếu là hình vuông, hai đường chéo bằng nhau (d₁ = d₂ = d). Khi đó, công thức diện tích hình thoi trở thành (d x d) / 2. Đồng thời, hình vuông cũng là hình chữ nhật có bốn cạnh bằng nhau, diện tích là cạnh x cạnh (a x a). Liệu có mối liên hệ nào giữa d và a trong hình vuông không? (Gợi ý: dùng định lý Pytago, nhưng cái này là kiến thức lớp lớn hơn).
- Hình Tam giác: Việc suy luận công thức diện tích hình thoi dựa vào chia nó thành 4 tam giác vuông bằng nhau và xét diện tích của chúng. Công thức diện tích tam giác là (đáy x chiều cao) / 2.
Việc liên kết kiến thức giúp em có cái nhìn tổng quan hơn về thế giới hình học, thấy được sự logic và mối quan hệ giữa các hình dạng khác nhau. Điều này rất quan trọng cho việc phát triển tư duy toán học.
Có một khái niệm trong kinh doanh mà tôi nghĩ có thể so sánh một cách tương đối, đó là công thức tính tỷ trọng. Tỷ trọng cho biết một phần chiếm bao nhiêu phần trăm trong tổng thể. Tương tự, khi ta chia hình thoi thành các tam giác nhỏ để tính diện tích, ta đang xem xét “tỷ trọng” diện tích của mỗi phần nhỏ so với diện tích toàn bộ hình thoi. Dù khác lĩnh vực, nhưng cách tư duy phân tích một tổng thể thành các phần nhỏ để hiểu rõ hơn thì khá giống nhau.
Lời Khuyên Cho Phụ Huynh Hỗ Trợ Con Học Diện Tích Hình Thoi Lớp 4
Đối với các bậc phụ huynh, việc đồng hành cùng con học toán lớp 4, đặc biệt là các khái niệm mới như diện tích hình thoi lớp 4, là rất quan trọng. Dưới đây là một vài lời khuyên nhỏ:
- Đừng gây áp lực: Quan trọng nhất là tạo không khí học tập thoải mái, vui vẻ cho con. Hãy khen ngợi những nỗ lực của con hơn là chỉ tập trung vào kết quả đúng sai.
- Sử dụng đồ dùng trực quan: Cắt giấy hình thoi, dùng que tính để làm đường chéo, hoặc vẽ hình thoi trên cát, trên bảng… để con dễ hình dung. Mô hình thực tế luôn hiệu quả hơn chỉ nhìn hình vẽ trong sách.
- Liên hệ với cuộc sống: Cùng con tìm kiếm các vật dụng hình thoi trong nhà, khi đi siêu thị hoặc khi xem tivi. Hỏi con xem đó là hình gì và liệu có thể ước lượng diện tích của nó được không.
- Giải thích “vì sao”: Thay vì chỉ bắt con học thuộc công thức, hãy cố gắng giải thích cho con hiểu tại sao công thức lại như vậy (dựa vào hình chữ nhật như đã nêu ở trên). Điều này kích thích tư duy và giúp con nhớ lâu hơn.
- Làm bài tập cùng con: Dành thời gian làm bài tập cùng con, không chỉ là đưa đáp án mà hãy hướng dẫn con cách suy nghĩ, cách trình bày bài giải.
- Kiên nhẫn: Mỗi đứa trẻ có tốc độ tiếp thu khác nhau. Nếu con chưa hiểu ngay, đừng vội nản lòng. Hãy thử giải thích bằng cách khác hoặc cho con nghỉ ngơi một chút rồi quay lại.
Hỗ trợ con học toán không chỉ giúp con nắm vững kiến thức mà còn xây dựng sự tự tin và tình yêu với môn học này.
Các ứng dụng của hình thoi trong đời sống giúp hiểu về diện tích hình thoi lớp 4
Mở Rộng: Chu Vi Hình Thoi
Mặc dù bài viết này tập trung vào diện tích hình thoi lớp 4, nhưng chúng ta cũng nên biết một chút về chu vi hình thoi. Chu vi là tổng độ dài các cạnh bao quanh hình. Vì hình thoi có bốn cạnh bằng nhau, nên công thức tính chu vi hình thoi rất đơn giản:
Chu vi = Độ dài cạnh x 4
Nếu gọi độ dài cạnh hình thoi là a, thì Chu vi P = a x 4.
Việc phân biệt rõ giữa diện tích (phần mặt phẳng bên trong) và chu vi (đường bao quanh) là rất quan trọng khi học hình học. Diện tích dùng để đo lường bề mặt, còn chu vi dùng để đo lường độ dài đường viền.
Đôi khi trong quá trình học, chúng ta có thể gặp phải những khái niệm mới mẻ hoặc khó hiểu, giống như khi gặp thông báo không thể truy cập trang web này trên máy tính. Ban đầu có thể thấy bối rối, nhưng bằng cách tìm hiểu nguyên nhân (kiểm tra lại công thức, xem xét các đặc điểm của hình, hỏi thầy cô/bố mẹ), chúng ta sẽ tìm được cách “truy cập” và giải quyết vấn đề.
Trong một thế giới ngày càng kết nối và số hóa, việc hiểu các khái niệm cơ bản, dù là toán học hay công nghệ (như hàng order nghĩa la gì trong thương mại điện tử) đều giúp chúng ta hòa nhập và làm chủ cuộc sống tốt hơn. Toán học rèn luyện tư duy logic, khả năng giải quyết vấn đề, những kỹ năng cần thiết cho mọi lĩnh vực, dù là học tập, công việc hay cuộc sống hàng ngày.
Tóm Lược Lại Kiến Thức Trọng Tâm
Vậy là chúng ta đã cùng nhau đi một vòng khám phá về hình thoi và cách tính diện tích của nó ở cấp độ lớp 4. Hãy cùng tóm tắt lại những điểm cốt lõi nhé:
- Hình thoi là tứ giác có 4 cạnh bằng nhau, các cặp cạnh đối song song, các góc đối bằng nhau, hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường.
- Công thức tính diện tích hình thoi lớp 4 là: S = (d₁ x d₂) / 2, trong đó d₁ và d₂ là độ dài hai đường chéo.
- Công thức này có thể suy luận dễ dàng dựa trên việc đặt hình thoi vào trong một hình chữ nhật.
- Khi tính toán, luôn chú ý đến đơn vị đo và đảm bảo chúng cùng loại trước khi thực hiện phép nhân.
- Diện tích có đơn vị là đơn vị độ dài vuông (cm², dm², m²…).
- Tránh nhầm lẫn công thức diện tích hình thoi với các hình khác và đừng quên bước chia 2.
- Hình thoi xuất hiện nhiều trong đời sống quanh ta.
- Hiểu nguồn gốc, thực hành thường xuyên và liên kết kiến thức với các hình khác là những cách hiệu quả để nhớ lâu công thức.
Việc nắm vững cách tính diện tích hình thoi lớp 4 không chỉ giúp em hoàn thành tốt các bài tập trên lớp mà còn xây dựng nền tảng toán học vững chắc cho tương lai. Hãy luyện tập thường xuyên, đừng ngại hỏi khi chưa hiểu, và quan trọng nhất là hãy tận hưởng niềm vui khi khám phá những điều mới mẻ trong toán học! Kiến thức về diện tích hình thoi lớp 4 chỉ là bước khởi đầu trên hành trình chinh phục thế giới toán học đầy màu sắc và logic. Chúc các em học tốt và luôn giữ vững tinh thần ham học hỏi!