Nhớ lại thời đi học, có lẽ ai trong chúng ta cũng từng “đau đầu” với đủ loại hình học, từ hình vuông, hình tròn, đến tam giác. Mỗi hình một vẻ, mỗi hình lại đòi hỏi một cách tính khác nhau. Nhưng có một loại tam giác khá đặc biệt mà lại xuất hiện rất nhiều trong đời sống và cả trong các bài toán, đó là tam giác vuông cân. Và câu hỏi mà nhiều người đặt ra là làm thế nào để tính Công Thức Tính Diện Tích Tam Giác Vuông Cân một cách nhanh chóng và chính xác nhất?
Bạn biết không, việc nắm vững các công thức cơ bản trong toán học không chỉ giúp chúng ta vượt qua các kỳ thi ở trường lớp, mà còn mở ra những góc nhìn mới về thế giới xung quanh. Từ việc thiết kế một khu vườn nhỏ xinh hình tam giác vuông cân, tính toán lượng vật liệu cần dùng cho một mái nhà, hay thậm chí là hiểu được nguyên lý đằng sau những thiết kế kiến trúc độc đáo, kiến thức về diện tích tam giác vuông cân đều có thể áp dụng.
Bài viết này không chỉ đơn thuần là liệt kê các công thức. Chúng ta sẽ cùng nhau “mổ xẻ” xem tam giác vuông cân có gì đặc biệt, tại sao lại có những công thức đó, và làm thế nào để áp dụng chúng vào thực tế một cách “ngọt” nhất. Hãy cùng BSS Việt Nam khám phá hành trình thú vị này nhé!
Tam Giác Vuông Cân Là Gì?
Tam giác vuông cân là một hình đặc biệt trong thế giới hình học phẳng.
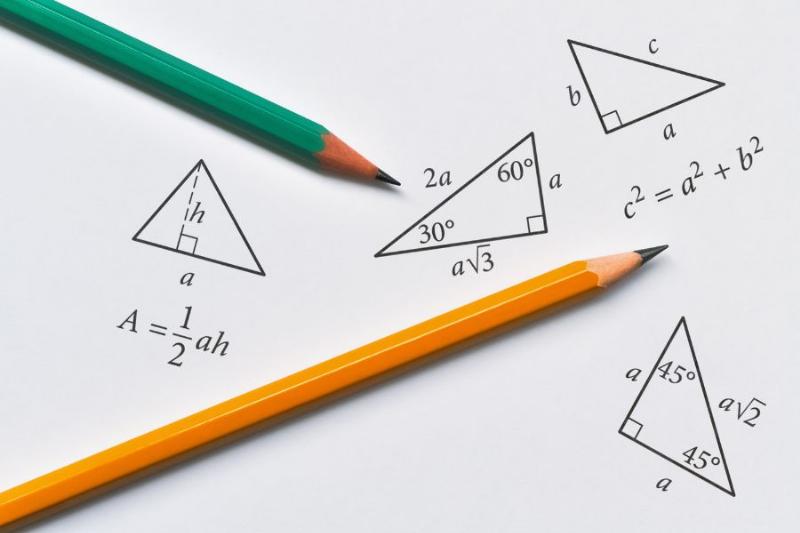
Nó là sự kết hợp độc đáo giữa tính chất của tam giác vuông (có một góc 90 độ) và tính chất của tam giác cân (có hai cạnh bằng nhau). Cụ thể, tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.
Hãy hình dung một góc nhà vuông vắn (90 độ). Nếu bạn vẽ một đường thẳng cắt ngang góc đó sao cho khoảng cách từ điểm cắt trên tường này đến đỉnh góc bằng khoảng cách từ điểm cắt trên tường kia đến đỉnh góc, và nối hai điểm cắt đó lại, bạn sẽ tạo ra một tam giác vuông cân. Hai cạnh “tường” chính là hai cạnh góc vuông bằng nhau, và cạnh “cắt ngang” là cạnh huyền. Góc giữa hai cạnh tường là góc vuông (90 độ), và hai góc còn lại (góc kề cạnh huyền) luôn bằng nhau và bằng 45 độ. Tổng ba góc dĩ nhiên vẫn là 180 độ như mọi tam giác khác.
Vì Sao Cần Biết Công Thức Tính Diện Tích Tam Giác Vuông Cân?
Biết công thức tính diện tích tam giác vuông cân giúp giải quyết nhiều bài toán học và các vấn đề thực tế liên quan đến không gian và vật liệu.
Từ việc giải các bài tập trong sách giáo khoa, chuẩn bị cho các kỳ thi, đến việc áp dụng vào các lĩnh vực như kiến trúc, xây dựng, thiết kế nội thất, may mặc, hay thậm chí là các dự án thủ công đơn giản tại nhà, việc tính toán diện tích tam giác vuông cân là cần thiết. Nó giúp chúng ta định lượng không gian, ước tính chi phí vật liệu, hoặc đơn giản là hiểu rõ hơn về các hình dạng quanh mình. Giống như việc biết cách tính chiều dài hình chữ nhật giúp bạn đo đạc đất đai hay lên kế hoạch lát sàn, nắm vững công thức này sẽ mở ra nhiều ứng dụng bất ngờ.
Cuộc sống luôn đầy rẫy những vấn đề cần giải quyết, và đôi khi, chìa khóa lại nằm ở những kiến thức nền tảng nhất. Việc tính toán diện tích, thể tích hay chu vi là những kỹ năng cơ bản giúp chúng ta định lượng và kiểm soát các yếu tố vật lý trong thế giới thực. Đối với tam giác vuông cân, một hình dạng tưởng chừng chỉ có trong sách vở, nhưng thực tế lại xuất hiện rất nhiều trong các cấu trúc, hoa văn, và thiết kế. Hiểu rõ cách tính diện tích của nó giúp chúng ta đưa ra quyết định chính xác hơn, tiết kiệm thời gian và nguồn lực.
Công Thức Tính Diện Tích Tam Giác Vuông Cân
Đây là phần trọng tâm mà nhiều người tìm kiếm: Làm thế nào để tính diện tích của một tam giác vuông cân? Có hai cách tiếp cận chính, tùy thuộc vào thông tin bạn đã biết về tam giác đó.
Công Thức Cơ Bản Dựa Vào Cạnh Góc Vuông
Cách phổ biến và dễ hiểu nhất để tính diện tích tam giác vuông cân là dựa vào độ dài của hai cạnh góc vuông (vì chúng bằng nhau).
Diện tích tam giác nói chung được tính bằng công thức: (1/2) đáy chiều cao. Trong tam giác vuông, hai cạnh góc vuông đóng vai trò là đáy và chiều cao tương ứng.
Vì tam giác vuông cân có hai cạnh góc vuông bằng nhau, gọi độ dài cạnh góc vuông là ‘a’. Khi đó, diện tích (S) sẽ là:
$$ S = frac{1}{2} times text{cạnh góc vuông} times text{cạnh góc vuông} $$
$$ S = frac{1}{2} times a times a $$
$$ S = frac{1}{2} a^2 $$
Đây là công thức tính diện tích tam giác vuông cân đơn giản nhất, chỉ cần biết độ dài một cạnh góc vuông là tính được ngay.
- Ví dụ 1: Một miếng gỗ hình tam giác vuông cân có cạnh góc vuông dài 10 cm. Tính diện tích miếng gỗ đó.
- Bước 1: Xác định độ dài cạnh góc vuông: a = 10 cm.
- Bước 2: Áp dụng công thức S = (1/2)a².
- Bước 3: Tính toán: S = (1/2) 10² = (1/2) 100 = 50 cm².
- Vậy, diện tích miếng gỗ là 50 cm². Thật đơn giản phải không nào?
Công Thức Dựa Vào Cạnh Huyền
Đôi khi, chúng ta lại biết độ dài cạnh huyền mà không biết độ dài cạnh góc vuông. Liệu có cách nào để tính diện tích trong trường hợp này không? Hoàn toàn có! Chúng ta sẽ sử dụng một công cụ toán học quen thuộc: Định lý Pytago.
Định lý Pytago phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Gọi cạnh huyền là ‘c’, và hai cạnh góc vuông là ‘a’ (vì chúng bằng nhau). Theo định lý Pytago, ta có:
$$ a^2 + a^2 = c^2 $$
$$ 2a^2 = c^2 $$
$$ a^2 = frac{c^2}{2} $$
Bây giờ, nhìn lại công thức tính diện tích dựa vào cạnh góc vuông: S = (1/2)a². Chúng ta đã tìm được giá trị của a² theo c². Chỉ cần thay thế vào công thức diện tích:
$$ S = frac{1}{2} times a^2 $$
$$ S = frac{1}{2} times frac{c^2}{2} $$
$$ S = frac{c^2}{4} $$
Đây là công thức tính diện tích tam giác vuông cân khi biết độ dài cạnh huyền ‘c’.
- Ví dụ 2: Một tấm vải hình tam giác vuông cân có cạnh huyền dài 20 cm. Tính diện tích tấm vải đó.
- Bước 1: Xác định độ dài cạnh huyền: c = 20 cm.
- Bước 2: Áp dụng công thức S = c²/4.
- Bước 3: Tính toán: S = 20² / 4 = 400 / 4 = 100 cm².
- Vậy, diện tích tấm vải là 100 cm².
 Hinh minh hoa tam giac vuong can voi canh huyen c va cach tinh dien tich
Hinh minh hoa tam giac vuong can voi canh huyen c va cach tinh dien tich
So Sánh Hai Công Thức
Bạn thấy đấy, chúng ta có hai công thức chính để tính diện tích tam giác vuông cân:
- S = (1/2)a² (với ‘a’ là độ dài cạnh góc vuông)
- S = c²/4 (với ‘c’ là độ dài cạnh huyền)
Việc lựa chọn công thức nào hoàn toàn phụ thuộc vào dữ kiện bạn có. Nếu đề bài cho cạnh góc vuông, dùng công thức 1. Nếu cho cạnh huyền, dùng công thức 2. Cả hai đều cho kết quả chính xác.
Việc hiểu cách suy ra công thức từ định lý Pytago không chỉ giúp bạn nhớ lâu hơn mà còn rèn luyện khả năng suy luận logic, một kỹ năng cực kỳ quan trọng không chỉ trong toán học mà còn trong giải quyết các vấn đề kinh doanh phức tạp. Tương tự như việc hiểu các ký hiệu bản đồ có mấy loại giúp bạn đọc bản đồ hiệu quả, việc hiểu nguồn gốc công thức giúp bạn áp dụng linh hoạt hơn.
Ứng Dụng Thực Tế Của Việc Tính Diện Tích Tam Giác Vuông Cân
Bạn có bao giờ tự hỏi, liệu những công thức toán học khô khan này có thực sự được áp dụng vào cuộc sống hàng ngày không? Với công thức tính diện tích tam giác vuông cân, câu trả lời là CÓ, và rất nhiều nữa là đằng khác!
Hãy nhìn quanh nhà bạn xem. Một số mái nhà có thể có hình dạng tam giác vuông cân (đặc biệt là các phần mái hiên nhỏ). Khi cần sửa chữa hoặc lợp lại phần mái này, việc tính diện tích sẽ giúp bạn biết cần mua bao nhiêu tấm lợp.
Trong thiết kế nội thất, nhiều chi tiết trang trí, gạch lát sàn, hoặc thậm chí là cách sắp xếp đồ đạc có thể tạo ra các hình tam giác vuông cân. Việc tính diện tích giúp kiến trúc sư hoặc gia chủ ước lượng vật liệu cần thiết, từ số lượng gạch men cho đến lượng sơn.
Các sản phẩm thủ công, như chăn vá (patchwork) hay đồ handmade, thường sử dụng các mảnh vải hình tam giác để ghép lại thành hoa văn. Nếu bạn muốn tạo ra một hoa văn đối xứng từ các tam giác vuông cân, việc tính diện tích từng mảnh sẽ giúp bạn dự trù được tổng diện tích cần thiết cho dự án.
Ngay cả trong những lĩnh vực tưởng chừng không liên quan như ẩm thực, đôi khi việc cắt một chiếc bánh pizza hình vuông thành các lát hình tam giác vuông cân cũng đòi hỏi một sự hiểu biết nhất định về hình học để đảm bảo các lát cắt đều nhau.
Việc áp dụng kiến thức toán học vào thực tế giúp chúng ta nhìn nhận thế giới một cách có cấu trúc và logic hơn. Nó tương tự như cách sơ đồ tư duy toán giúp chúng ta tổ chức kiến thức và giải quyết vấn đề một cách hệ thống.
Lời Khuyên Từ Chuyên Gia
Để hiểu rõ hơn về tầm quan trọng của việc nắm vững các kiến thức cơ bản như công thức tính diện tích tam giác vuông cân, chúng ta hãy cùng lắng nghe chia sẻ từ một chuyên gia.
Tiến sĩ Lê Văn An, chuyên gia toán ứng dụng tại một viện nghiên cứu uy tín, cho biết: “Nhiều người nghĩ toán học chỉ dành cho những bộ óc siêu phàm, nhưng thực tế, toán học là nền tảng cho tư duy logic và giải quyết vấn đề. Việc thành thạo những công thức cơ bản như tính diện tích tam giác vuông cân không chỉ là làm được bài tập, mà là rèn luyện khả năng phân tích, suy luận từ dữ kiện đã cho để tìm ra kết quả. Kỹ năng này cực kỳ hữu ích trong mọi lĩnh vực, từ khoa học, kỹ thuật đến kinh doanh. Một người có khả năng phân tích tốt sẽ nhìn nhận vấn đề một cách toàn diện hơn và đưa ra giải pháp hiệu quả.”
Lời khuyên của Tiến sĩ An nhấn mạnh rằng, việc học toán không chỉ là học vẹt công thức, mà là học cách tư duy.
 Ung dung thuc te cua viec tinh dien tich tam giac vuong can trong doi song
Ung dung thuc te cua viec tinh dien tich tam giac vuong can trong doi song
Những Sai Lầm Thường Gặp Khi Tính Diện Tích Tam Giác Vuông Cân
Mặc dù công thức tính diện tích tam giác vuông cân khá đơn giản, nhưng đôi khi chúng ta vẫn có thể mắc phải những sai lầm không đáng có.
Sai lầm phổ biến nhất là nhầm lẫn giữa cạnh góc vuông và cạnh huyền. Hãy luôn nhớ rằng cạnh huyền là cạnh dài nhất và đối diện với góc vuông. Hai cạnh còn lại (bằng nhau) là cạnh góc vuông. Nếu dùng nhầm giá trị vào công thức, kết quả sẽ hoàn toàn sai lệch.
Một lỗi khác là quên mất hệ số (1/2) trong công thức S = (1/2)a² hoặc nhầm lẫn giữa a² và c² trong công thức S = c²/4. Hãy kiểm tra kỹ lại công thức trước khi thực hiện phép tính.
Đơn vị đo lường cũng là một vấn đề cần lưu ý. Nếu cạnh được đo bằng centimet, diện tích sẽ là centimet vuông (cm²). Nếu đo bằng mét, diện tích là mét vuông (m²). Đảm bảo bạn sử dụng đơn vị nhất quán và ghi đúng đơn vị trong kết quả cuối cùng. Điều này quan trọng như việc hiểu phát biểu nào sau đây về tính chất của các đường sức điện là không đúng trong vật lý vậy, một sự nhầm lẫn nhỏ có thể dẫn đến kết quả sai hoàn toàn.
Cuối cùng, đừng quên kiểm tra lại các phép tính số học của mình. Đôi khi, lỗi bấm máy tính hoặc tính nhẩm sai lại là nguyên nhân chính dẫn đến kết quả không chính xác.
Các Bài Toán Nâng Cao Hơn
Sau khi đã nắm vững công thức tính diện tích tam giác vuông cân cơ bản, bạn có thể gặp các bài toán “biến tấu” hơn một chút.
Chẳng hạn, thay vì cho trực tiếp độ dài cạnh, đề bài có thể cho chu vi, hoặc tọa độ các đỉnh của tam giác trên mặt phẳng tọa độ. Khi đó, bạn cần áp dụng thêm các công thức khác để tìm ra độ dài cạnh góc vuông hoặc cạnh huyền trước khi áp dụng công thức tính diện tích.
Ví dụ, nếu biết chu vi của tam giác vuông cân là P, và gọi cạnh góc vuông là ‘a’, cạnh huyền là ‘c’. Ta có P = 2a + c. Sử dụng định lý Pytago, c = a√2. Thay vào công thức chu vi: P = 2a + a√2 = a(2 + √2). Từ đó suy ra a = P / (2 + √2). Sau khi tìm được ‘a’, ta áp dụng S = (1/2)a² để tính diện tích.
Hay nếu đề bài cho tọa độ 3 đỉnh A, B, C của tam giác, bạn cần sử dụng công thức tính khoảng cách giữa hai điểm để tìm độ dài các cạnh AB, BC, CA. Sau đó kiểm tra xem tam giác ABC có phải là tam giác vuông cân hay không (dựa vào độ dài các cạnh và định lý Pytago, hoặc dựa vào độ dốc của các đường thẳng để kiểm tra góc vuông), và cuối cùng áp dụng công thức tính diện tích phù hợp.
Những bài toán này đòi hỏi sự kết hợp nhiều kiến thức, không chỉ riêng công thức tính diện tích tam giác vuông cân. Nó giống như việc trong âm nhạc, để tạo ra một bản hòa âm hay, bạn cần hiểu rõ nhiều yếu tố khác nhau, không chỉ riêng độ to của âm phụ thuộc vào yếu tố nào. Sự kết hợp kiến thức là chìa khóa để giải quyết những vấn đề phức tạp hơn.
Việc luyện tập với các dạng bài tập khác nhau giúp củng cố kiến thức và nâng cao kỹ năng giải quyết vấn đề của bạn. Đừng ngại thử sức với những bài toán khó hơn một chút, đó là cách tốt nhất để tiến bộ.
Kết Luận
Qua bài viết này, chúng ta đã cùng nhau khám phá chi tiết về tam giác vuông cân và các cách tính diện tích của nó. Dù bạn biết độ dài cạnh góc vuông hay cạnh huyền, đều có công thức tính diện tích tam giác vuông cân phù hợp để bạn áp dụng: S = (1/2)a² hoặc S = c²/4.
Việc nắm vững những công thức cơ bản này không chỉ giúp bạn giải quyết tốt các bài toán học, mà còn trang bị cho bạn khả năng định lượng và phân tích không gian trong nhiều tình huống thực tế. Từ những dự án nhỏ trong gia đình đến việc hiểu các nguyên lý trong kiến trúc hay thiết kế, kiến thức về diện tích tam giác vuông cân đều có vai trò nhất định.
Hy vọng những chia sẻ này từ BSS Việt Nam đã giúp bạn cảm thấy tự tin hơn khi đối mặt với các bài toán hoặc tình huống cần tính diện tích tam giác vuông cân. Đừng ngần ngại thực hành với các ví dụ khác nhau và áp dụng vào các tình huống thực tế bạn gặp trong cuộc sống. Kiến thức chỉ thực sự trở nên hữu ích khi chúng ta biết cách vận dụng nó! Chúc bạn thành công!
